在 《索引的故事：正排索引与倒排索引简介》 中，我们提到过倒排索引的实现主要面临着 4 个问题：

  • 分词形成的词项（term）可能是海量的，需要可以在内存和磁盘上高效存储；
  • 既然词项是海量的，那么如何快速找到对应的词项也是个问题；
  • 每个词项对应的文档数可能非常多，也就是上图中文档列表的链表很长；
  • 在词项对应的文档多的情况下，多个文档列表间做交集的效率将是个挑战。

这四个问题可以分为两个方面：词项方面的问题和文档列表方面的问题。在 Lucene 的倒排索引的实现中，其使用词项索引（Term Index）来解决上述 1 和 2 的问题，而对于 3 和 4，Lucene 对数据进行了压缩处理，使用 Roaring Bitmaps、跳表等技术来进行快速求交集。

今天这一节内容我们就来深入了解一下倒排索引的实现，看看上面的问题都有哪些技术选型可以解决。

倒排索引的组成主要有 3 个部分（如下图）：Term Index、Term Dictionary 和 Posting List。其中，Term Dictionary 保存的是词项，随着词项越来越多，从 Term Dictionary 中查找一个词项势必越来越慢，所以必须对这些词项做索引，从而有了 Term Index，它是 Term Dictionary 的索引，最好设计得越小越好，这样缓存在内存中也没有压力。Posting List 保存着每个词项对应的文档 ID 列表（其实还有其他信息，这里为了方便理解，只显示 ID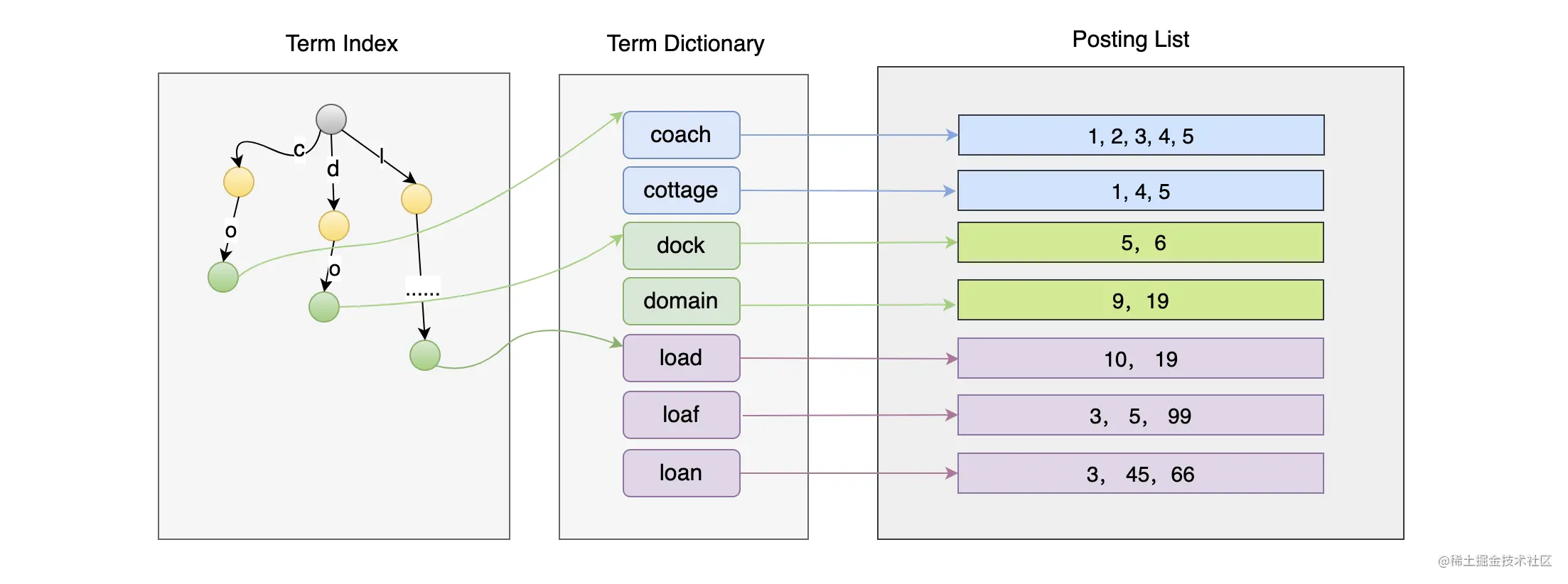）。 倒排索引设计.png 为了让你对 Lucene 的设计有个全局的认识，在了解 Term Index、Term Dictionary、Posting List 的具体实现前，我们先来看看 Segment、文档、Field、Term 与它们的关系。在之前的章节内容中我们已经了解过 ES 中相关的概念了，我们知道，默认的情况下，ES 每秒都会把缓存中的数据写入到 Segment，然后根据某些规则进行刷盘，并且合并这些 Segment。所以 Segment 数据一旦写入就不变了，采用不变性的设计主要有以下两个原因：一个是更新数据对磁盘来说并不友好，另一个是可变的数据会有并发写的问题。

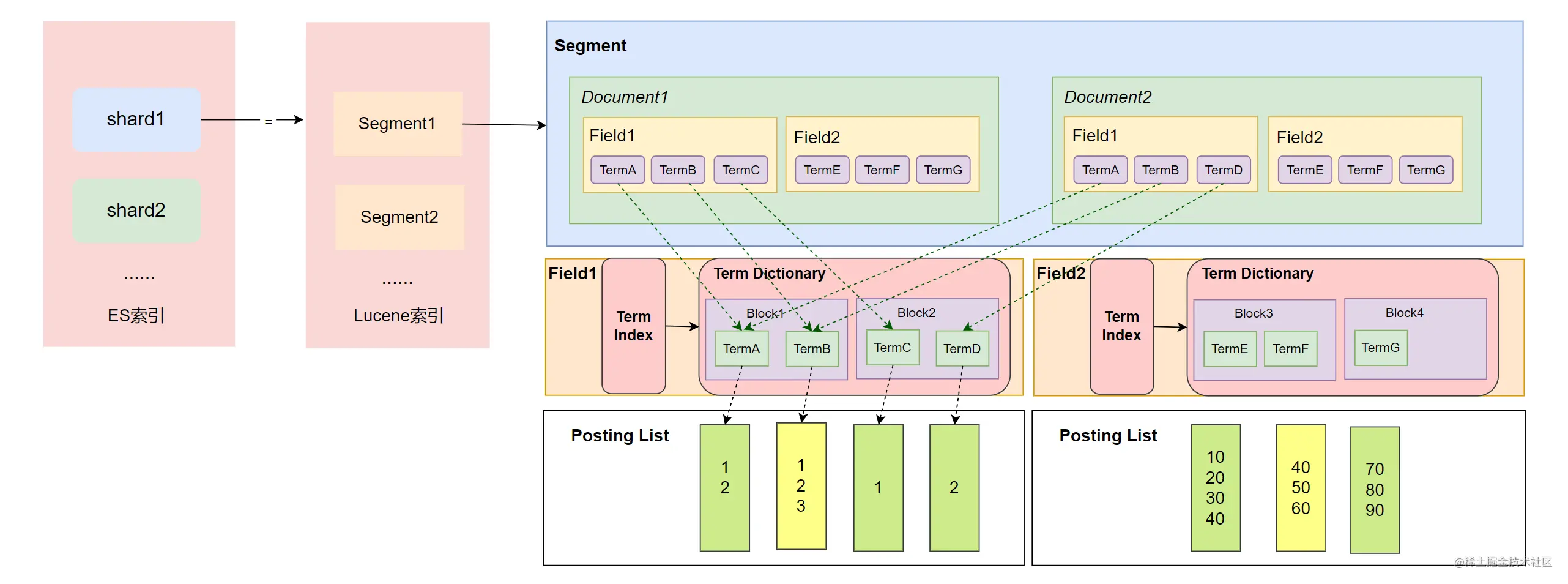
逻辑上，一个 Segment 上会有多个文档，一个文档有多个字段（Field）。如下图中的 Segment 就有两个文档，文档 1 和 2 都有两个 Field。这些字段的内容会被分词器形成多个 Term，然后以块的形式保存在 Term Dictionary 中，并且系统会对 Term Dictionary 的内容做索引形成 Term Index。在搜索的时候，通过 Term Index 找到 Block 后进一步找到 Term 对应的 Posting List 中的文档 ID，然后计算出符合条件的文档 ID 列表进行返回。需要注意的是，Segment 中的每个字段（Field）都会有自己的 Term Index、Term Dictionary、Posting List 结构，也就是说在每个 Field 中这些结构都是独立的，图中也表达得非常明显了！

各概念间的关系图.png

一、Term Index 的实现

Term Index 作为 Term Dictionary 的索引，其最好资源消耗小，可以缓存在内存中，而且数据查找要有较低的复杂度。在讨论 Term Index 如何实现前，先来看看下面几个词语：

  1. coach、cottage
  2. dock、domain

这两对词语分别有着公共的前缀：co 和 do。如果我们把 Term Dictionary 中的 Term 排序后按公共前缀抽取出来按块存储，而 Term Index 只使用公共前缀做索引，那本身要存储 coach、cottage 两个字符串的索引，现在只需要存储 co 一个就行了。这样的话，拥有同一公共前缀的 Term 越多，实际上就越省空间，并且这种设计在查找的时候复杂度是公共前缀的长度：O(len(prefix)) 。

但是这样的索引有个缺点，它只能找到公共前缀所在的块的地址，所以它既无法判断这个 Term 是否存在，也不知道这个 Term 保存在 Term Dictionary（.tim）文件的具体哪个位置上。 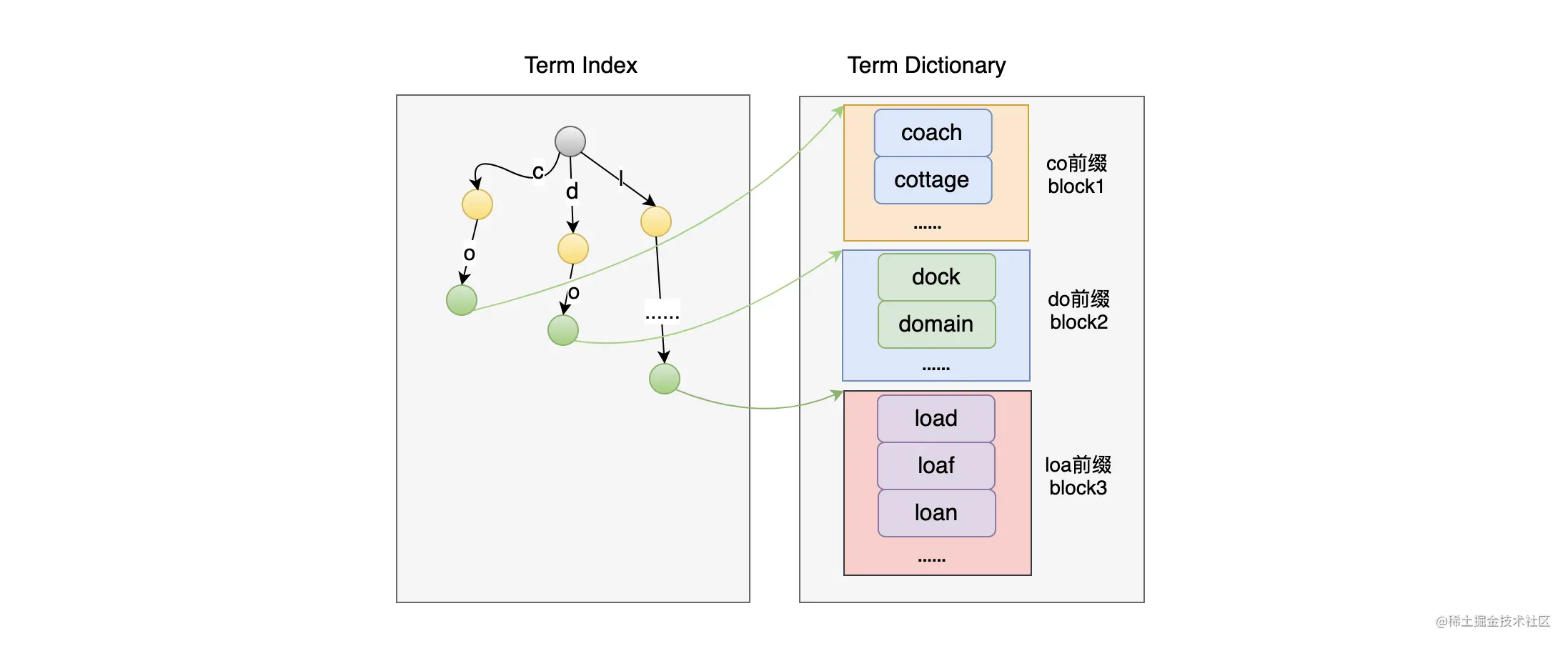TermIndex的实现.png 如上图，对于在每个块中如何快速查找到对应的 Term，我们可以使用二分法来搜索，因为 Block 中的数据是有序的。但机智的你是不是也发现可以优化的地方了？因为前缀在 Term Index 中保存了，那么 Block 中就不需要为每个 Term 再保存对应的前缀了，所以 Block中保存的每个 Term 都可以省略掉前缀了，比如，co 前缀的 block1 中保存的内容为 ach、ttage 即可。

对于前缀索引的实现，业界使用了 FST 算法来解决。FST（Finite State Transducers）是一种 FSM（Finite State Machines，有限状态机），并且有着类似于 Trie 树的结构。下面来简单了解一下 FST。

FST 有以下的特点：

  • 通过对 Term Dictionary 数据的前缀复用，压缩了存储空间；
  • 高效的查询性能，O(len(prefix))的复杂度；
  • 构建后不可变。（事实上，倒排索引一旦生成就不可变了。）

下图是一个简单的 FST 图，从图中可以看出，一条边有两个元素 label 和 out，其中 label 为 key 的元素，例如 cat 这个 key 就有 c、a、t 这三个元素，out 为此边的值 value。小圆圈为 FST 的一个节点，节点分为两类——普通节点和 Final 节点，图中灰黑色的为 Final 节点，Final 节点中还有 Finalout，代表 Final 节点的值。 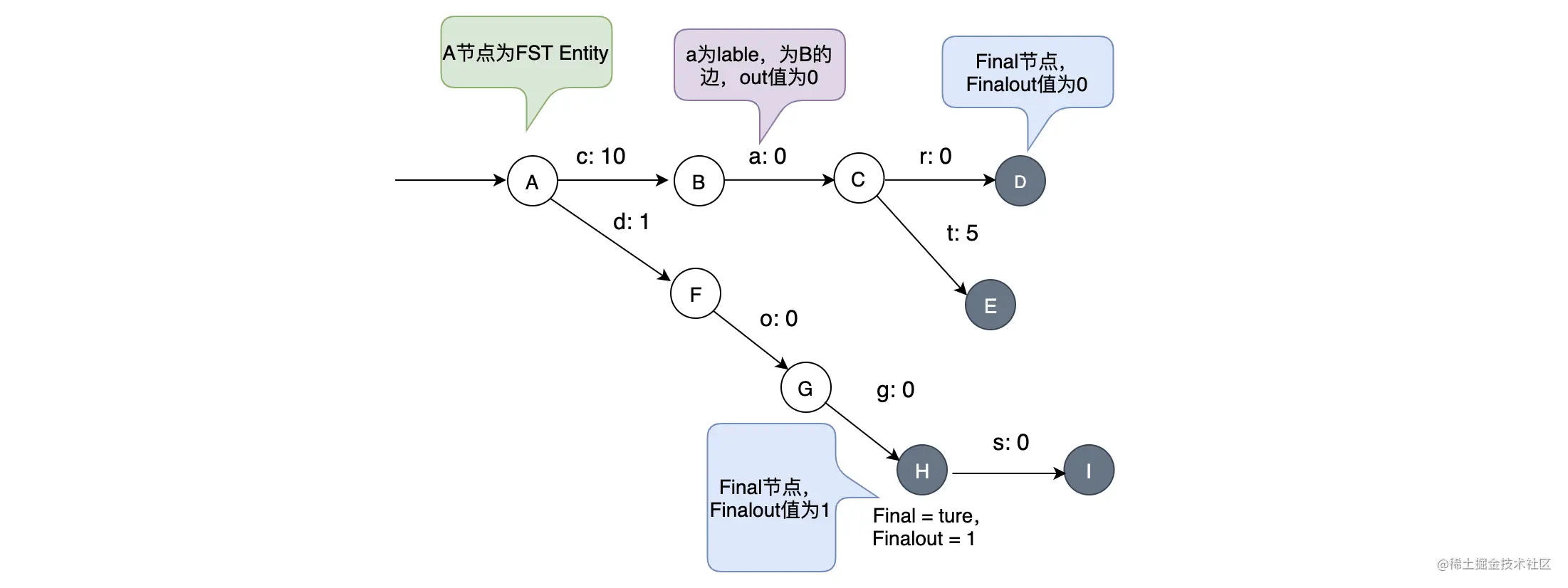FST元素简介.png 当访问 cat 的时候，读取 c、a、t 的值作和， 再加上 Final 节点的 Finalout 值即可：10 + 0 + 5 + 0 = 15；当访问 dog 的时候，读取 d、o、g 的值即可，但是由于 g 为 Final，所以需要加上 g 的 Finalout：1 + 0 + 0 + 1 = 2。

事实上，FST 是一种非常复杂的结构，但你可以把它理解为一个占用空间小且高效的 Key-Value 数据结构。Term Index 使用 FST 做实现带来了两个基本功能：

  • 快速试错，如果在 FST 上不存在，不需要再遍历整个 Term Dictionary；
  • 快速定位到 Block 的位置，经过 FST 的输出，可以算出 Block 在文件中的位置。

至此我们把 Term Index 的实现机制介绍得差不多了，下面来看一下 Term Dictionary 的实现。

二、Term Dictionary 的实现

在倒排索引组成的 3 个部分中，Term Dictionary 保存着 Term 与 Posting List 的关系，存储了 Term 相关的信息，如记录了包含该 Term 的文档数量（DocFreq）、Term 在整个 Segment 中出现的频率等，还保存了指向 Posting List 文件的指针（文档 ID 列表的位置、词频位置等）。

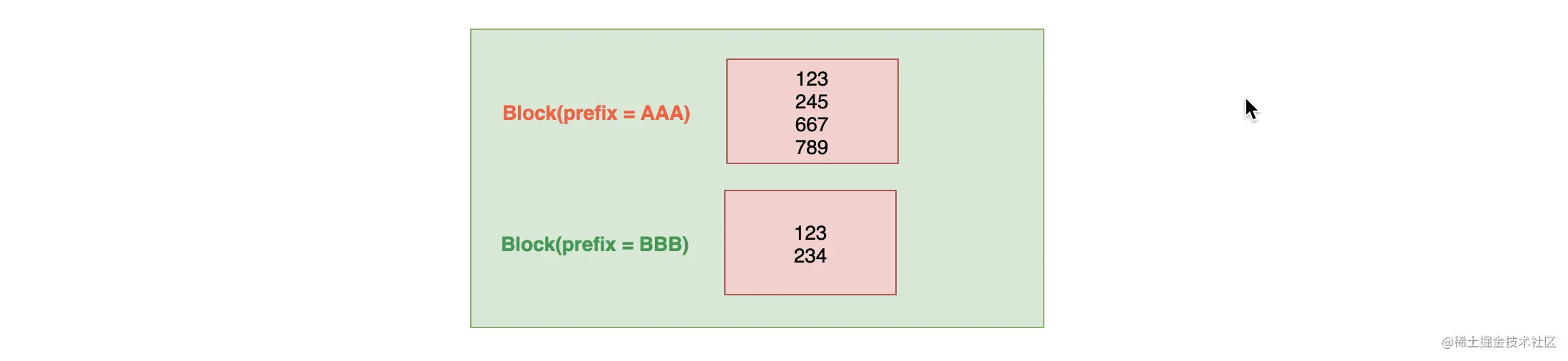
如下图，在对 Term Dictionary 做索引的时候，先将所有的 Term 进行排序，然后将 Term Dictionary 中有共同前缀的 Term 抽取出来进行分块存储，再对共同前缀做索引，最后通过索引就可以找到公共前缀对应的块在 Term Dictionary 文件中的偏移地址。 分块.png 由于每个块中都有共同前缀，所有不需要再保存每个Term的全部内容，只需要保存其后缀即可，而且这些后缀都是排好序的。 分块结果.png

至此，我们可以通过Term Index 和 Term Dictionary 快速判断一个 Term 是否存在，并且存在的时候还可以快速找到对应的 Posting List 信息。

三、Posting List 的实现

上面提到过 Posting List 并不只是包含文档的 ID，其实 Posting List 包含的信息比较多，如文档 ID、词频、位置等。Lucene 把这些数据分成 3 个文件进行存储：

  • .doc 文件，记录了文档 ID 信息和 Term 的词频，还额外记录了跳跃表的信息，用来加速文档 ID 的查询；并且还记录了 Term 在 pos 和 pay 文件中的位置，有助于进行快速读取。
  • .pay 文件，记录了 Payload 信息和 Term 在 doc 中的偏移信息；
  • .pos文件，记录了 Term 在 doc 中的位置信息。

因为倒排索引的主要目标就是要找到文档 ID，所以下面讨论 Posting List 的时候我们只关注文档 ID 的信息，其他的就忽略了。前面提到过，Posting List 主要面临着两个问题：

  • 如何节省存储？
  • 如何快速做交集？

要节省存储，可以对数据进行压缩存储；至于如何做交集，业界应用得比较多的是跳表、Roaring Bitmaps 等技术。下面我们就针对这两个问题以及对应的方法分别讲解下。

1. 节省存储：整型压缩

不知道你有没有留意过，其实 Int 类型或者 Long 类型是可以进行压缩的。我们可以根据需要处理的数据的取值范围，选择占用更小字节数的数据类型来存储原数据。例如下面的 Int 数组：

  1. # Int数组
  2. [8, 12, 100, 140]
  4. # 各个元素与其二进制表示
  5. 8 -> 00001000
  6. 12 -> 00001100
  7. 100 -> 01100100
  8. 140 -> 10001100

这个 Int 数组，如果每个数据都要用 4 个字节来保存的话，共需要 16 个字节。但你会发现，数组中最大的数 140 只需要用 8 位（一个字节）就可以表示了。这样一来，原本需要 16 个字节的数据现在只需要 4 个字节就可以表示了。

整数压缩基本就是这个思路了，当然还有其他的玩法（下面介绍的 VIntBlock），但核心的思想都是：用最少的位数表示原数据，并且兼顾数据读取效率。Lucene 在 Posting List 中使用了 2 种编码格式来对整数类型的数据进行压缩——PackedBlock 和 VIntBlock，并且在对整数进行压缩的基础上，还会对文档 ID 使用差值存储的方式来对数据做进一步的压缩处理。

PackedBlock

在 Lucene 中，每当处理完 128 个包含某个 Term 的文档时，就会将文档的 ID 和词频使用 PackedInts 进行压缩存储，生成一个 PackedBlock。PackedBlock 中有两个数组，一个是存储文档 ID 的，一个是存储词频的。所以 PackedBlock 是存储固定长度的整型数组的结构，且数组的长度为128。

下面简单介绍一下 PackedInts 的实现，PackedInts 会将 Int[] 压缩成为一个 Block，其压缩方式是把数组中最大的那个数占用的有效位数作为标准，然后各个元素打包的数组中，每个元素都按这个有效位数来算。例如下面数组：

  1. # Int数组
  2. [8, 12, 100, 120]
  4. # 各个元素与其二进制表示
  5. 8 -> 0001000
  6. 12 -> 0001100
  7. 100 -> 1100100
  8. 120 -> 1111000

最大数 120 的有效位数为 7，所以数组中所有数据都可以使用 7 位来表示。假设这个数组有 128 个元素，且最大为 120，那么这个压缩后的数组就会如下： PackedBlock.png

最终这个数组占用的位数为 7 bit * 128 = 896 bit = 112 字节（这里没有算 len 占用的空间，但请不要忽略 len 也是要花空间存储的），这比起原数据 128 * 4 字节 = 512 字节确实省了不少。

PackedBlock只能存储固定长度的数组数据，如果一个 Segment 的文档数不是 128 的整数倍，那该怎么办？这时可以用 VIntBlock 来进行存储。

VIntBlock

VIntBlock 通过使用变长整型编码方式来对数据进行压缩，所以其可以存储复合的数据类型，不再需要像 PackedInts 那样规定数据元素是多少位的。VIntBlock 采用 VInt 来对 Int 类型进行压缩，VInt 采用可变长的字节来表示一个整数，每个字节只使用第 1 到第 7 位来存储数据，第 8 位用来作为是否需要读取下一个字节的标记。 VInt.png 如上图，本身 Int 200 需要 4 个字节来进行存储，使用 VInt 后只需要 2 个字节即可。

使用 PackedBlock 与 VIntBlock 来解析 .doc 文件

Lucene 在处理文档的时候，每处理 128 篇文档就会将其对应的文档 ID 数组（docDeltaBuffer）和词频（TermFreq）数组（freqBuffer）处理为两个 Block：PackedDocDeltaBlock 和 PackedFreqBlock，并且使用 PackedInts 类对数据进行压缩存储，生成一个 PackedBlock。而把最后不足 128 篇文档的数据采用 VIntBlock 来存储（如果有 131 个文档，会生成一个 PackedBlock 和 3 个 VIntBlock）。并且在生成 PackedBlock 的时候，会生成跳表（SkipData），使得在读取数据时可以快速跳到指定的 PackedBlock。

下图为你整理了处理 .doc 文件的数据结构，以加深你对 Posting List 的理解。 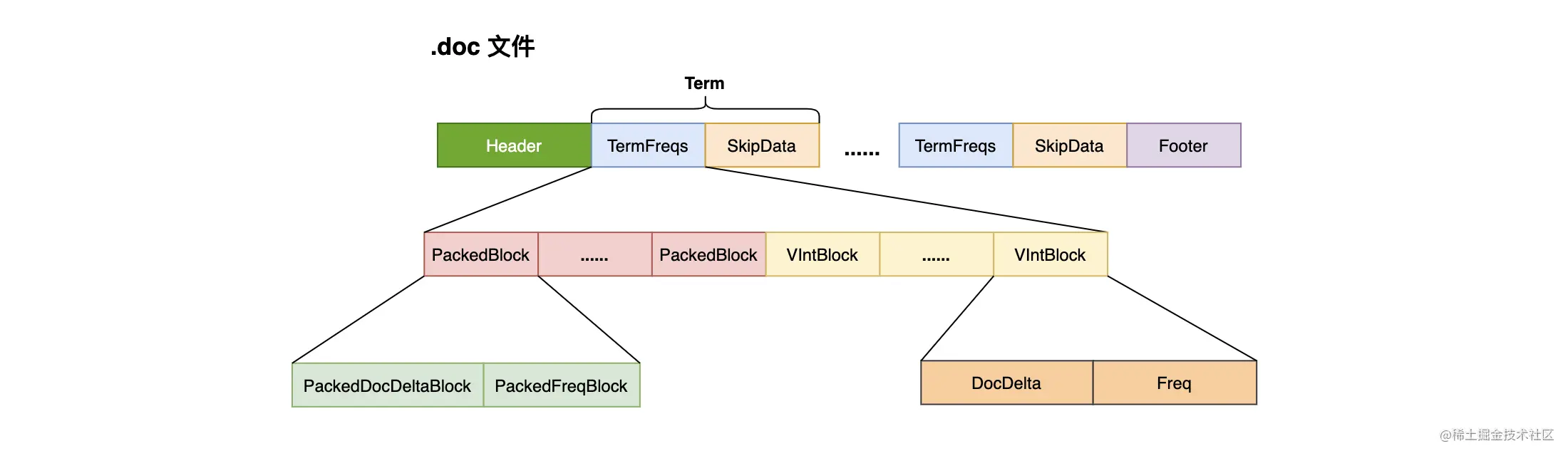doc文件格式.png

使用文档 ID 差值存储来节省空间

整数的压缩可以使单个数值占用的空间得以减少，但数与数之间还存在着微妙的关系，两个正整数的差一定会比它们中最大的那一个要小！

利用这个特性，我们可以使需要压缩的整数变成更小的数，从而进一步压缩空间。因为存储文档 ID 的数组是有序的（需要注意的是，词频是无序的，无法使用下面的处理方式），所以在保存文档 ID 的时候，docDeltaBuffer 中存的不是文档的 ID，而是与上一个文档 ID 的差值，这样做可以进一步压缩存储空间！

  1. ids = [1, 4, 6, 9, 14, 17, 21, 25]

如上面给定的数组 ids，如果用 PackedInts 的方式来对数据进行压缩的话，那么25（0001 1001）最少需要用 5 bit 来存储，所以整个数组需要 5 * 8 = 40 bit 来存储。如果数组中存储的是文档 ID 的差值，那么这个差值数组如下：

  1. dtIds = [1, 3, 2, 3, 5, 3, 4, 4]

dtIds 数组中最大值为 5（0000 0101），其最少需要 3 bit 来表示，那么整个数组只需要 3 * 8 = 24 bit，相对于原来需要 40 bit 来存储数据，差值存储的方式可以有效降低存储的空间。探其究竟，其实是两个正整数间的差值会比它们间最大的那个要小，那么需要的有效位数就可能会减少了。

其实综合了上面所有的流程，无非就是文档 ID 使用增量编码，数据分块存储、数据按需分配存储空间，而这整个过程叫做 FOR（Frame Of Reference） 。

2. 文档 ID 列表的交集求解

如果你需要检索朝代是唐代、诗人姓李、诗名中包含“明月”的诗，这时候系统会返回 3 条包含对应文档 ID 的列表，如下图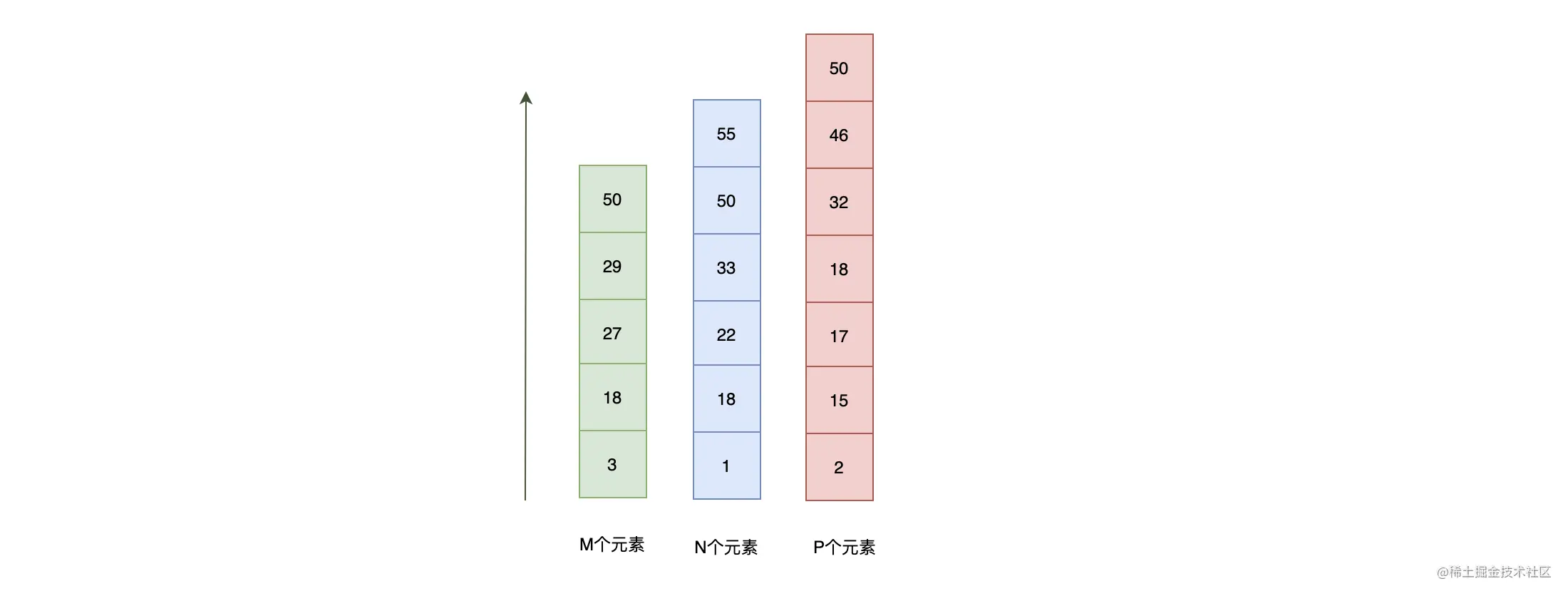： 交集.png 如果直接循环 3 个数组求交集，并不是很高效，下面对其进行优化。

位图

如果我们将列表的数据改造成位图会如何？假如有两个 posting list A 、B 和它们生成的位图如下：

  1. A = [2, 3, 5] => BitmapA = [0, 0, 1, 1, 0, 1]
  2. B = [1, 2, 5] => BitmapB = [0, 1, 1, 0, 0, 1]
  4. BitmapA AND BitmapB = [0, 0, 1, 0, 0, 1]

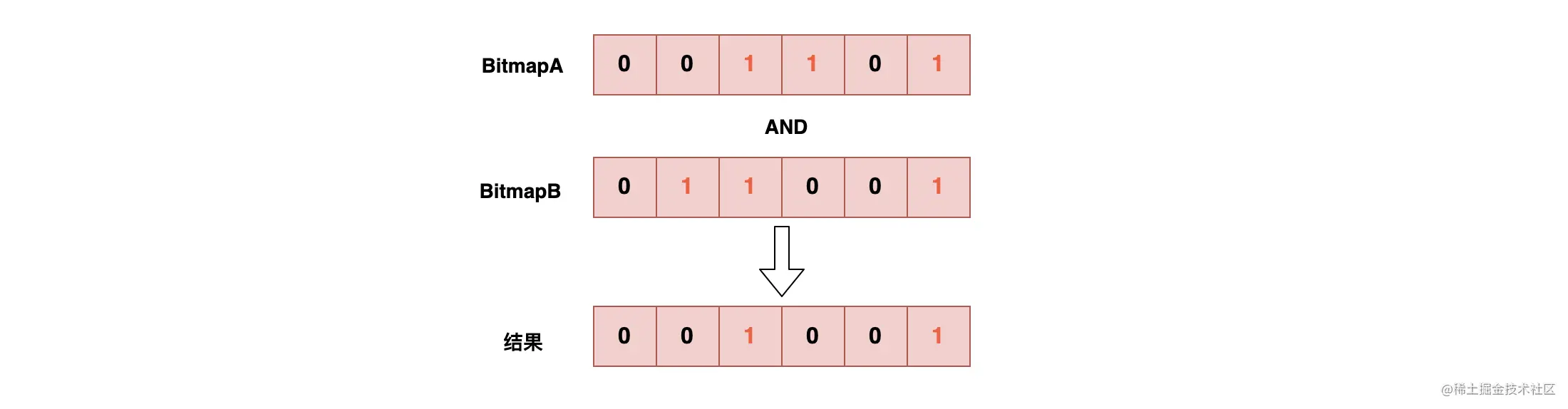
位与运算.png

生成位图的方法其实很简单：Bitmap[A[i]] = 1，其他为 0 即可。这样我们可以将 A、B 两个位图对应的位置直接做 AND 位运算，由于位图的长度是固定的，所以两个位图的 AND 运算的复杂度也是固定的，并且由于 CPU 执行位运算效率非常高，所以在位图不是特别大的情况下，使用位图求解交集是非常高效的。

但是位图也有其致命的弱点，总结下来有这几点：

  • 位图可能会消耗大量的空间。即使位图只需要 1 bit 就可以表示相对应的元素是否存在，但是如果列表中有一个元素特别大，例如数组 [1, 65535]，则需要 65535 bit 来表示。如果用 int32 类型的数组来表示的话，一个位图就需要 512M（2^32 bit = 2^29 Byte = 512M），如果有 N 个这样的列表，需要的存储空间为 N * 512M，这个空间开销是非常可怕的！

  • 位图只适合于数据稠密的场景。

  • 位图只适合存储简单整型类型的数据，对于复杂的对象类型无法处理，或者说复杂的类型本身就无法在 CPU 上直接使用 AND 这样的操作符。

业界中为了解决位图空间消耗大的问题，会使用一种压缩位图技术，也就是 Roaring Bitmap 来代替简单的位图。Roaring Bitmap 在业界应用广泛，下面来看看 Roaring Bitmap 的实现。

Roaring Bitmaps

它会把一个 32 位的整数分成两个部分：高 16 位和低 16 位。然后将高 16 位作为一个数值存储到有序数组里，这个数组的每一个元素都是一个块。而低 16 位则存储到 2^16 的位图中去，将对应的位置设置为 1。这样每个块对应一个位图，如下图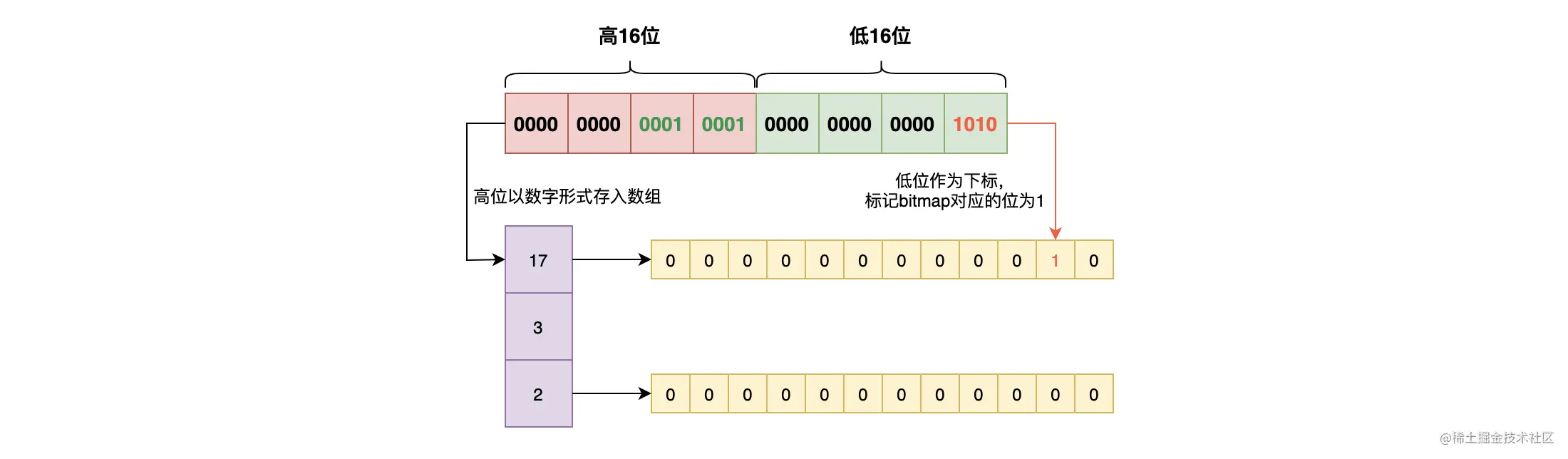： RoaringBitmaps.png Roaring Bitmaps 通过拆分数据，形成按需分配的有序数组 + Bitmaps 的形式来节省空间。其中一个 Bitmaps 最多 2^16 个 bit，共消耗 8K。而由于每个块中存的是整数，每个数需要 2 个字节来存储即可，这样的整数共有 2^16 个，所以有序数组最多消耗 2 Byte * 2^16 = 128K 的存储空间。由于存储块的有序数组是按需分配的，所以 Roaring Bitmaps 的存储空间由数据量来决定，而 Bitmaps 的存储空间则是由最大的数来决定。举个例子就是，数组[0, 2^32 - 1]，使用 Bitmaps 的话需要 512M 来存储，而 Roaring Bitmaps只需要 2 * (2 Byte + 8K)。

由于 Roaring Bitmaps 由有序数组加上 Bitmaps 构成，所以要确认一个数是否在 Roaring Bitmaps 中，需要通过两次查询才能得到结果。先以高 16 位在有序数组中进行二分查找，其复杂度为 O(log n)；如果存在，则再拿低 16 位在对应的 Bitmaps 中查找，判断对应的位置是否为 1 即可，此时复杂度为 O(1)。所以，Roaring Bitmaps 可以做到节省空间的同时，还有着高效的检索能力。

但是机智的你不知道有没有看出来，如果每个块的 Bitmaps 一直消耗 8K 的存储是不是超级浪费？如果这一个块中的数据很少，或者很稀疏，那还不如把 Bitmaps 做成数组呢。那到底用数组还是用 Bitmaps，阈值在哪里呢？当数据量达到 4096 的时候，我们发现 4096 * 16 bit(2 Byte) = 8K，所以当一个块的数据量小于 4096 的时候，可以使用 short 类型的有序数组存储数据，并且使用变长数组进一步节省空间。 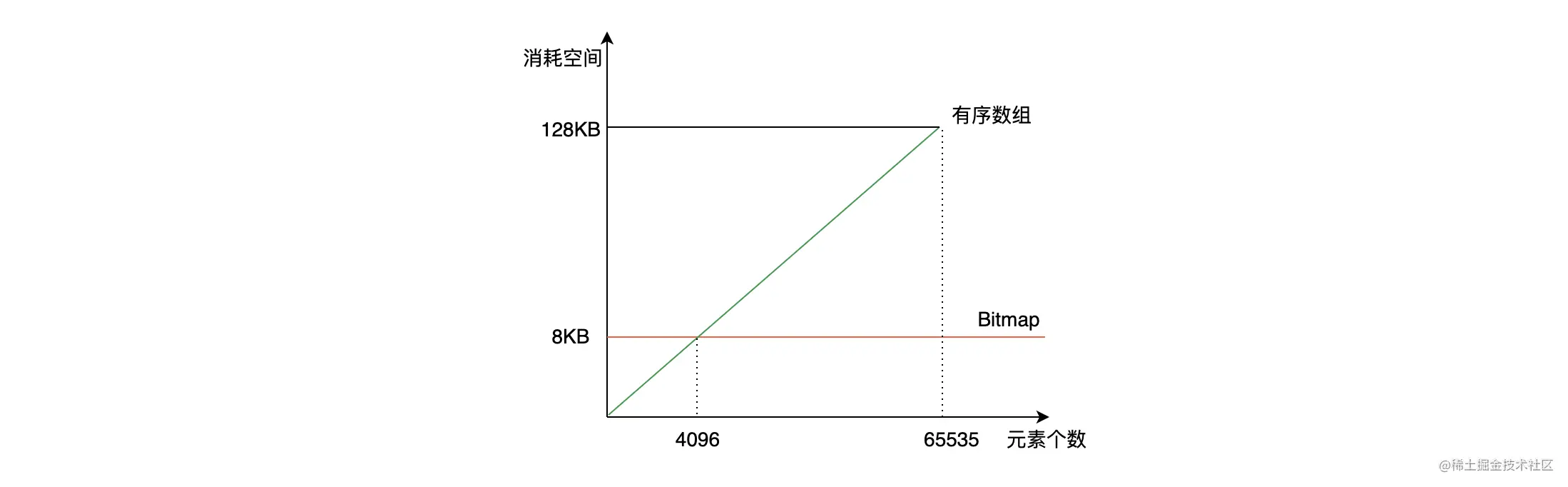Bitmap与有序数组的比较.png

业界除了使用 Roaring Bitmaps 来求交集外，还使用了跳表。

使用跳表加速多个列表交集的求解

跳表是一种有序的数据结构，它通过在每个节点中维持多个指向其他节点的索引，从而达到快速访问的目的。 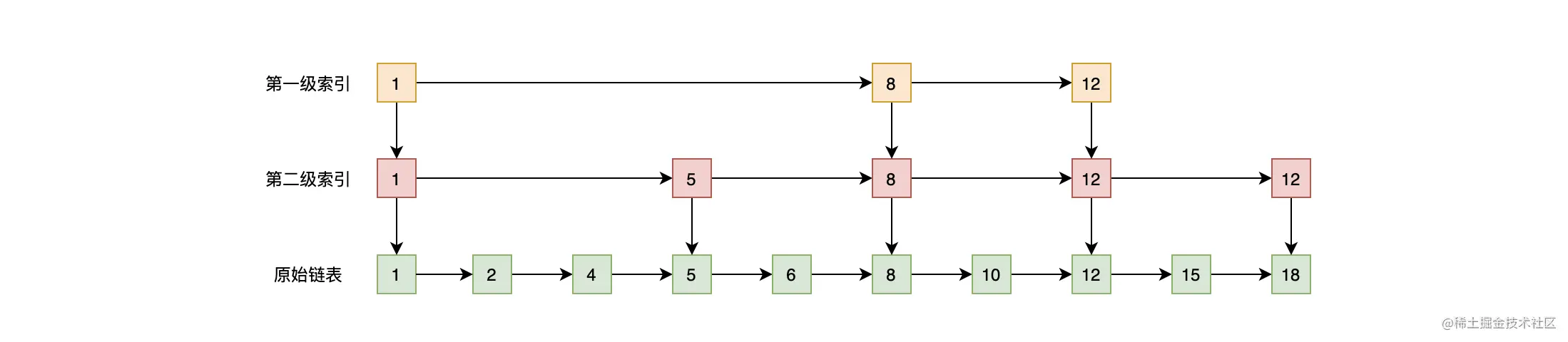简单的跳表.png

如上图，有序链表不能像有序数组那样使用二分法进行快速访问，但可以对有序链表维护一层或者多层索引使其快速访问。

在求解两个有序列表 A 和 B 的交集时，可以使用归并排序的方法来遍历两个列表，将复杂度从 O(M * N) 降低到 O(M + N)，这里的 M、N 分别为这两个列表的长度。

链表归并求交集的过程可以总结为以下三个步骤。

  • 第一步：将指针 p1 和 p2 分别指向列表 A 和 B 的开头。

  • 第二步：比较 p1 和 p2 指向的数据，会出现 3 种情况，如果内容相等，说明是公共元素，需要加入到结果集中；如果 p1 的内容小于 p2 的内容，p1 向后移；如果 p1 的内容大于 p2 的内容，p2 向后移。总结起来就是，谁小谁就往前走，相等就一起往前走，直到有一方结束！

  • 第三步：重复第二步，直到 p1 或者 p2 到达链表尾为止。

这里我们再结合以下示意图和例子来加深一下对归并流程的理解。指针 p1 和 p2 的原位置如下图所示，下面我们就来看看它们是怎么移动的。 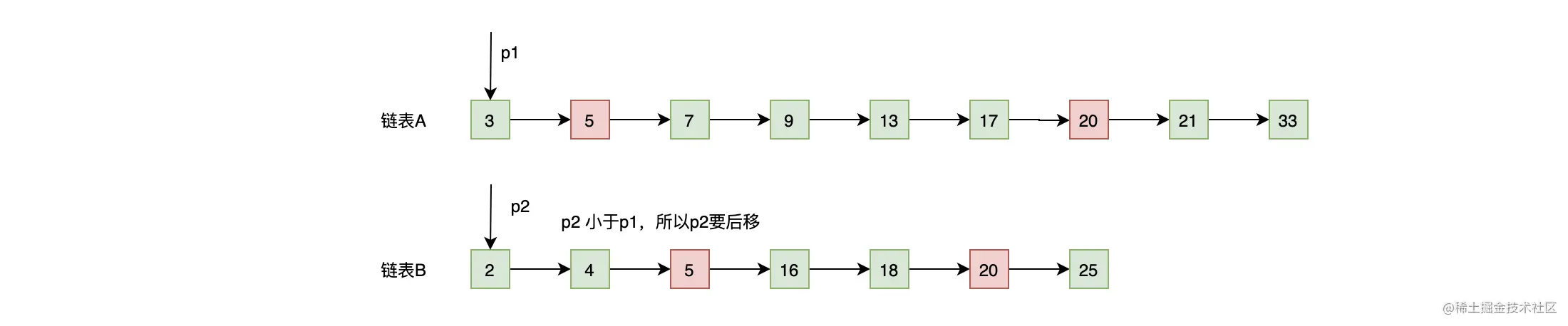归并1.png

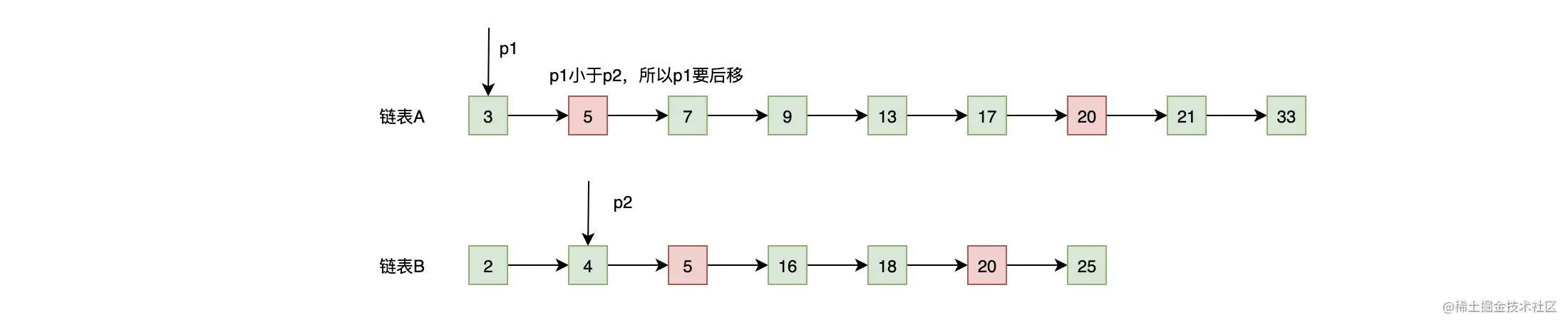
  1. p2 的内容小于 p1 的内容（2 < 3），基于谁小谁就往前走的原则，所以 p2 往后移动一位，移动后的结果如下图： 归并2.png
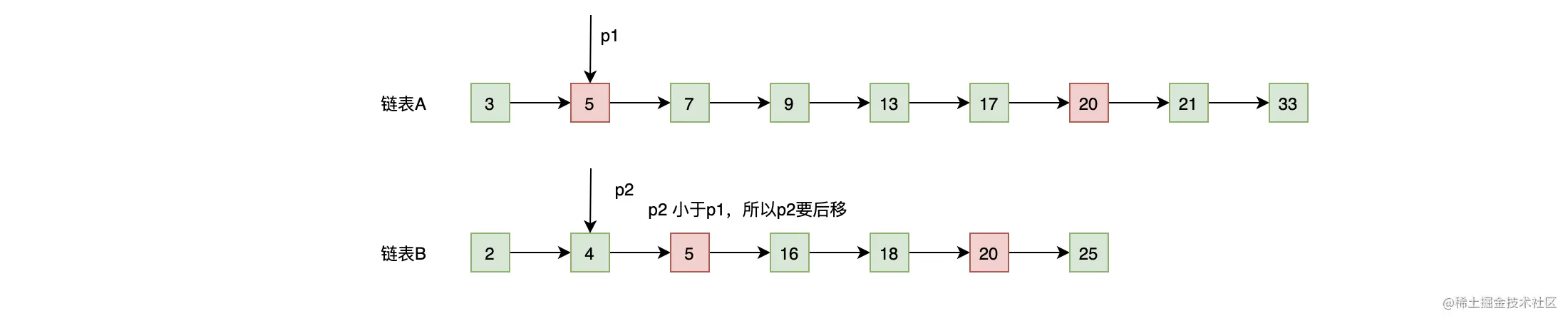
  2. p1 的内容小于 p2 的内容（3 < 4），基于谁小谁就往后走的原则，所以 p1 往后移动一位，移动后的结果如下图： 归并3.png
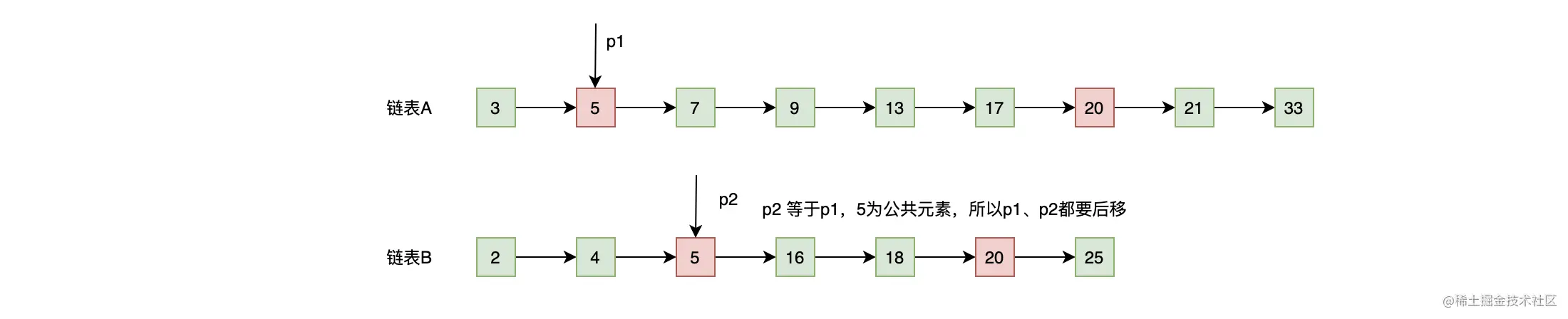
  3. p2 的内容小于 p1 的内容（4 < 5），基于谁小谁就往后走的原则，所以 p2 往后移动一位，移动后的结果如下图： 归并4.png
  4. p2 的内容等于 p1 的内容（5 = 5），所以 5 为公共元素，需要记录下来，并且基于相等就一起往后走的原则，所以 p2 和 p1 都往后移动一位，移动后的结果如下图： 归并5.png 就这样，一直继续上述的流程直到链表 B 结束。

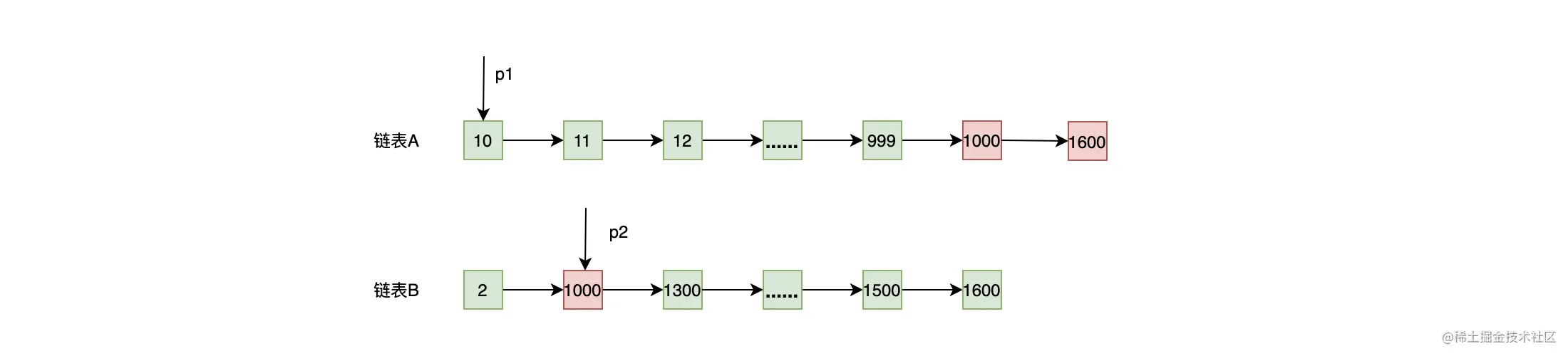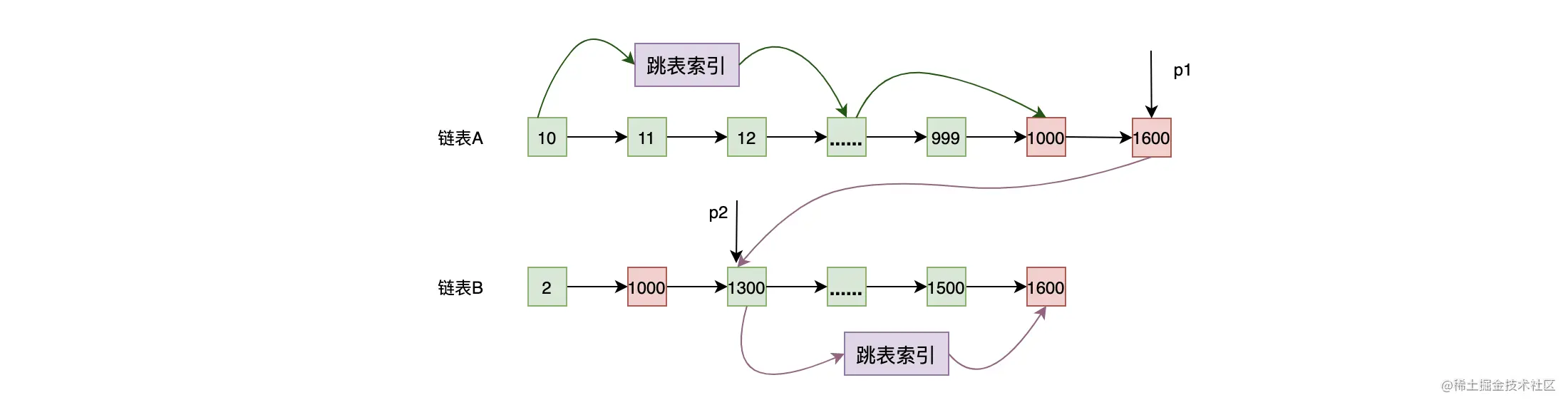归并排序的方式可以降低链表求交集的复杂度，但上述的算法还有优化的地方。从下图中可以看出，此时 p1 要从 10 开始找直到多次才能找到 1000 这个大于或者等于 p2 的元素。 归并优化.png 要优化这个问题，可以使用前面介绍的跳表，给链表做索引。下图中，p1 使用跳表索引经过比较少的次数就可以找到 1000 了。 归并使用跳表优化.png 那既然链表 A 和 B 都有跳表索引的结构，那在链表 B 中查找数据也同样可以使用跳表索引的结构进行加速。如下图，当 p1 的值大于链表 B 当前值时，用 p1 的值当作 key，在链表 B 中使用二分查找，这样 p2 就可以使用跳表索引快速往前跳了。 相互二分查找.png 这种二分查找法可以总结为：谁当前值大，就用其作为 key 到其他列表中做二分查找。但是，需要说明的是，虽然使用跳表索引可以降低查询的复杂度，但是跳表索引是要消耗空间的，并且在构建跳表的时候，也需要消耗额外的时间！

四、总结与思考

在这一讲中，我为你详细介绍了倒排索引的实现。ES 中的倒排索引主要分为 3 个部分：Term Index、Term Dictionary 和 Posting List。

  • Term Index 是 Term Dictionary 的索引，使用它可以快速判断一个 Term 是否存在，并且可以找到这个 Term 在 Term Dictionary 存储的块地址。Term Index 使用了 FST 来实现，其有着小巧且复杂度低的特点。

  • 而 Term Dictionary 是存储 Term 信息的地方，其内容包括 Term、包含该 Term 的文档的数量、Term 在整个 Segment 中出现的频率等。

  • 我们还学习了 Posting List 的实现，了解了 Lucene 使用 PackedBlock 和 VIntBlock 对整数进行压缩的思路，也介绍了业界使用 Roaring Bitmaps 和跳表来解决列表求交集的方案。

最后回到古诗词背诵大赛，我们可以使用正排索引去完成第一个项目，而第二个项目可以使用倒排索引完成，如果你感兴趣的话可以使用上述的数据结构来实现这个“机器人”。